邵博士科研随笔来自于赛思亿内部学习资料,主要是邵博士给技术人员有关技术基础的培训资料,挑选有代表性的发布,与业内的朋友共享。

傅里叶的那些事儿
“懂与不懂,都是收获”
背 景 介 绍
拉普拉斯变换和傅里叶变换是所有学习电气工程的同学心中永远的痛,因为其覆盖的课程包括且不限于“基本电路理论”、“积分变换”、“自动控制原理”和“信号与系统”等。就邵博士个人而言,当时的学习有2个很直观的感觉,一来在学习过程中,完全陷入了拉普拉斯和傅里叶变换的数学公式的记忆和运算中了,二来根本搞不清这两货的区别是什么,感觉就是拉普拉斯更加高级一些而已。
作为一种经验的提炼,或者说仅仅作为一本学习笔记,本文档总结一下傅里叶变化对于赛思亿的工作中的一些作用。需要说明的是,本文档的观点都是邵博士个人观点,并不说明这些观点都是正确的。
什么是傅里叶级数
虽然大家喜欢说傅里叶变换,但是意义更为明显的是傅里叶级数,也称为FS(Fourier series)。傅里叶用数学的方式,告诉我们任何周期函数都可以用正弦函数和余弦函数,及其频率倍数正弦函数和余弦函数的无穷级数来表示。
考虑到:
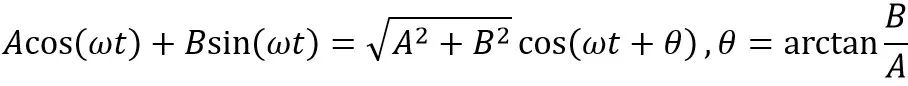
那么再简单一些,傅里叶级数告诉我们任何周期函数都可以用某一频率的余弦函数及其频率倍数的余弦函数的无穷级数来表示。
换一种语言说,傅里叶级数告诉我们,一个周期函数,由一系列的Acos(nωt+θ)组成,其中:
1、A是这一频率的余弦函数的幅值;
2、n = 0, 1, 2……;
3、ω是这个余弦函数的频率;
4、θ是这个余弦函数的相位;
进一步,特别考察n:
1、当n = 0时,这个余弦函数体现的是直流分量;
2、当n = 1时,这个余弦函数体现的是基波分量,往往是有用的值;
3、当n > 1时,这个余弦函数体现的是谐波分量;
所以用人话来说,傅里叶级数告诉我们:任何周期函数,都是由直流分量、单独的基波分量和大量的谐波分量组成。
傅里叶变换是傅里叶级数的一种特殊数学变换,是针对非周期函数而言的。本文档不做展开。
什么是频域
傅里叶级数比拉普拉斯高级得多的地方,在于傅里叶级数不仅仅是一种数学变换,而是创造了一种哲学,构筑了一个从另外一种视角审视信号的方法,那就是:频域!
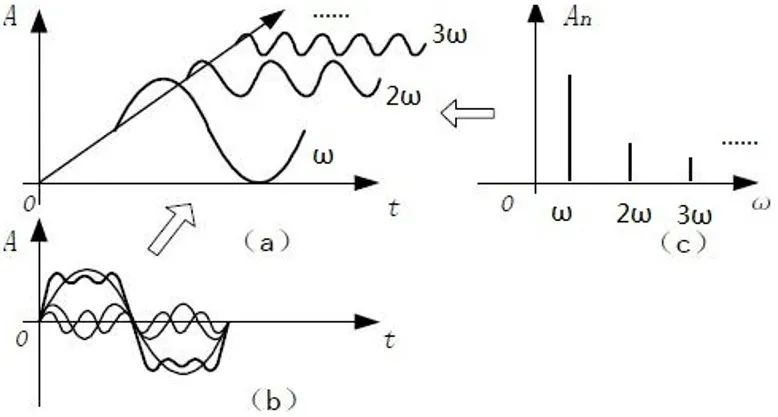
图表 1 时域和频域
从“知乎”上找到了一个很直观的图,见图表1,来说明一下同一种信号,可以从两个维度来理解,分别是时域和频域。
从时域上来说,任何信号随着时间t变化的幅度效果,能体现出他的性质;或者呢,将任何周期信号拆解成大量周期性变化的函数的叠加也是一种思路,这些周期的倒数就是频率,这样周期信号变成了大量频率的叠加。
频域提供了一个很新颖的理解事物的角度。例如:时域上一个模糊不清的“马鞍形”信号,可能在频域里面看到,是清晰的基波和三次谐波的叠加。
频域非常高明,已经深入人心。频域分析已经是一种哲学,一种信仰的存在了。

让·巴普蒂斯·约瑟夫·傅里叶 Baron Jean Baptiste Joseph Fourier 1768 ~ 1830
傅里叶是法国人,也曾跟着拿破仑混过。他最早将他的理论应用于热传导上面,结果在将论文递交给巴黎科学院的时候,被拒了。拒掉他的那些大牛中,就有一个叫拉普拉斯的。从这件事情上,我们可以得出:
1、18到19世纪的法国,是多么的灿烂辉煌。
2、法国人对法国人自己,也真是不客气。
3、即便论文被拒,即便理论不能被世界上大多数人所认可,这些并无损于傅里叶的伟大。

海因里希・鲁道夫・赫兹 Heinrich Rudolf Hertz 1857~1894
时域用时间来描述,其基本单位是s,而频域用频率(或者角频率)来描述,其基本单位是Hz。说到Hz,必须要提到赫兹。令人意外的是,赫兹先生比2位法国先贤晚出生了快100年。
时域分析一个小例子
赛思亿常常做谐波分析,因为所有船级社都会对谐波有一定的要求。简单地参考C42-A-095《江苏蓝德海上风电作业平台电力推进系统电网电压谐波分析》,可以看到,要分析正弦波的波形质量,从时域看到的信息有限,只有从频域分析每一个频率点,才可以更为公正地评价波形的正弦性。
从图表2可以看到,采用赛思亿的变频器,最大谐波源在于开关频率(2.5kHz)附近以及开关频率的2倍(5kHz)附近。
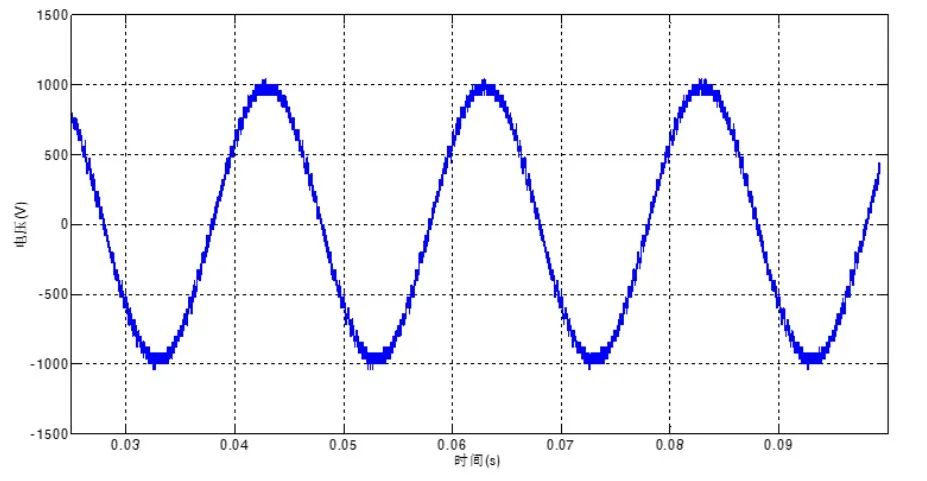
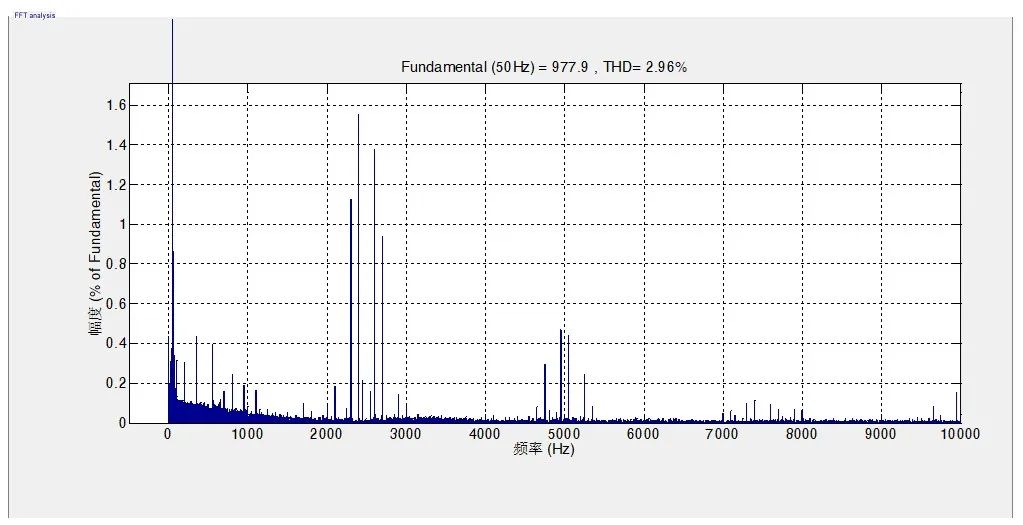
图表 2 时域和频域的转换(上图是时域波形,下图是频域波形)
从傅里叶级数到FFT
由于实际采集的时域时间总是有限的,任何一个周期时域波形,实战中都会因为采集长度的影响而在一定程度上呈现出非周期性,因此傅里叶级数仅具备理论上的意义,几乎不具备实战作用。
事实上,更实用一些的工具,是针对于非周期(实际是解决了有限时长问题)的时域波形进行傅里叶变换,也叫做FT(Fourier Transform)。
然而FT还是不那么实用,因为实际上现在的模拟量信号都已经通过数字化处理进行了采集,本质上已经不是连续信号了,而是采样周期相同的离散信号。针对离散信号的傅里叶变换,称为离散傅里叶变换,也叫做DFT(Discrete Fourier Transform)。
DFT已经实用了,虽然各种好,但是有一个缺点,就是计算量太大。数据长度足够大或者要求的频率分隔足够精细,导致了指数级增加的运算量而变得不可行。这个时候,快速傅里叶变换出现了,这就是注明的FFT(Fast Fourier Transform),其实就是采用了类似蝶形运算等一系列偷鸡的方法完成了时域到频域的转换。
经历了FS→FT→DFT→FFT的过程,虽然大家现在做谐波分析都是用FFT,但是实际上其背后的本质却是傅里叶级数。
要理解实用的DFT或者FFT,本身就是一门非常深奥的科学了,邵博士没有精力更没有能力展开。但是无论如何,离散化之后,会出现所谓的“频谱泄露”等问题,这些问题以后有机会再聊。
最后,赛思亿实际做谐波分析的时候,都是用示波器进行采集。为了让有限的时长尽量体现出周期性,一般赛思亿要求示波器的采集周期为10周期。
线性时不变系统
线性时不变系统是一个很洗脑的概念。和傅里叶级数一样,这个系统理论很完美,实际几乎不存在。这个概念确实在“基本电路理论”、“自动控制原理”和“信号与系统”几门学科中被反复强调。
这里不对线性时不变系统进行深入探讨,简单地说,用电阻、电感和电容等组成的系统就是线性时不变系统,二极管这种东西就不算。
一个典型的线性时不变系统的举例及其分析
假设有如图表3的一个电路。
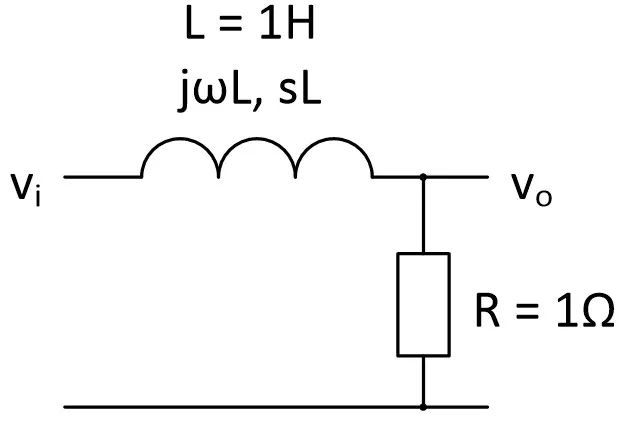
图表 3 一个典型的线性时不变电路
电阻是最有道德的、纯粹的和脱离低级趣味的,因为在任何场合,他就是本色不改,就是用R来描述。但是电感和电容就不是这么看待这个世界的了。
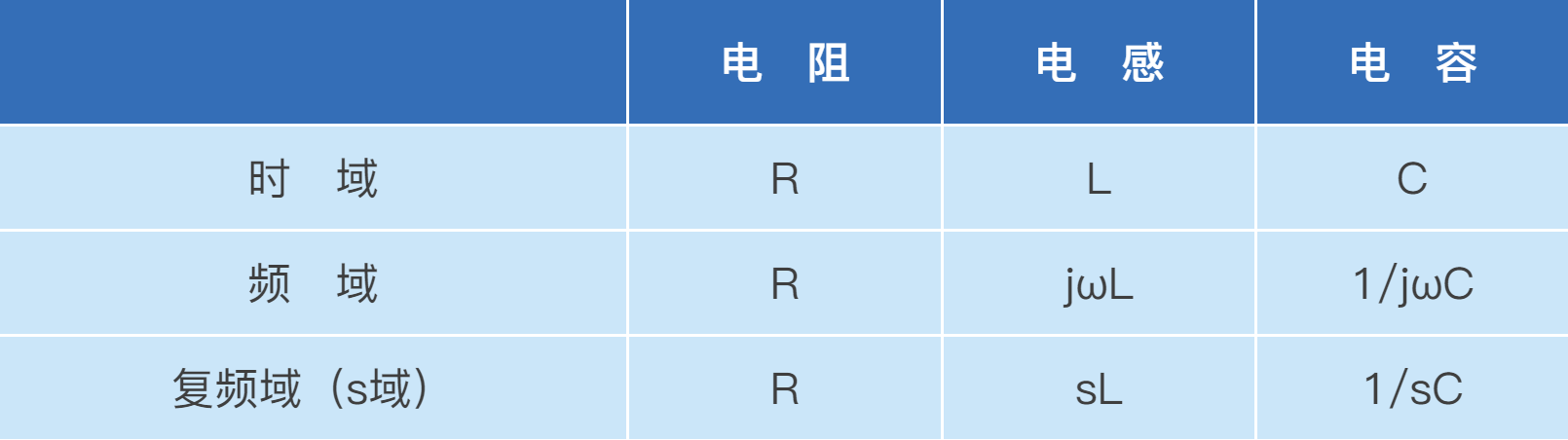
表格 1 电阻、电感和电容
从这个角度上来说,如果站在前面提到的s域,理解图表3所描绘的系统函数,则有:
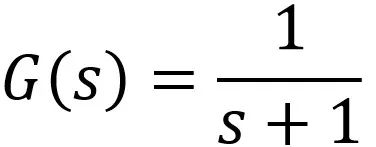
如果站在频域,理解图表3所描绘的频域响应,则有:
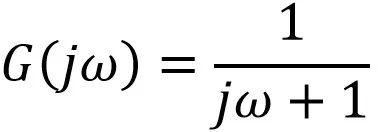
如果对此频域响应拆解,可以得到所谓的频域幅度响应和频域相位响应,即:
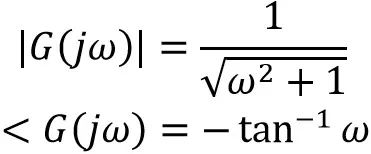
假设输入vi的是频率为ω的余弦函数,进入到了这个G(jω)之后,输出vo会有不同的幅值变化和相角变化(从上面公式来说,这个变化本身和ω有关),但是输出vo的频率仍然不会变化,是ω。
前面提到,傅里叶级数认为,所有的周期信号可以认为是不同频率的余弦函数之和表示。那么输入信号vi只要是周期信号,必然可以变成大量不同频率的余弦函数之和(频率分别是0,ω,2ω,……,Nω,……),每一个频率为Nω的输入都能对应一个频率为Nω的输出,只不过相位都不一样罢了,那么其输出vo可以认为是这些频率为Nω的输出的和。这个叫做线性系统的叠加原理。
上面的话可能看不清楚,这里举一个算例。
假设输入vi= cost + cos(3t)。考察输出vo。
我们首先考察cost输入图表3所示的网络会如何。再次频域幅度响应和频域相位响应,即:
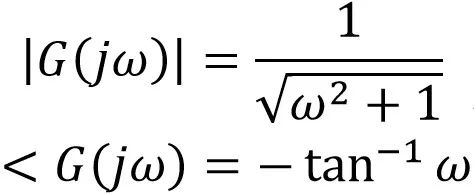
显然,此时ω = 1,那么:
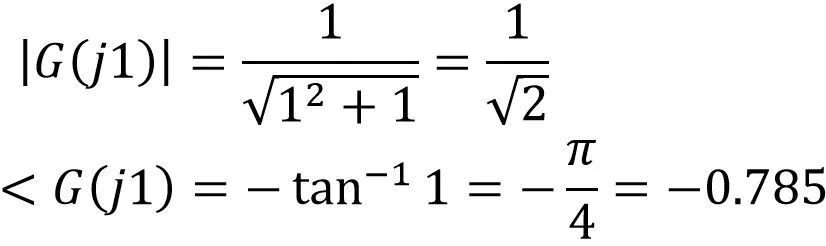
幅值衰减了,相角滞后了。那么输入cost对应的输出就是:
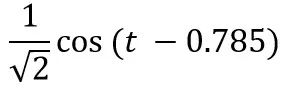
类似地,当ω = 3,那么:
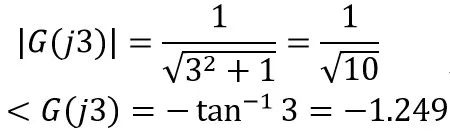
那么输入cos(3t)对应的输出就是:
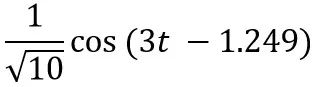
所以最终的输出vo是:
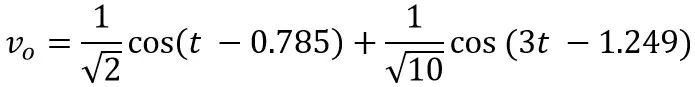
在这个计算过程中,我们完全不需要考虑输出信号的频率,而只要关心这个输出信号的幅值和相角究竟啥状态就行了。
波特图
如果我们遍历ω从0到+∞,可以得到针对每一个频率ω的幅值-频率响应(简称“幅频响应”)和相角-频率响应(简称“相频响应”),则可以得到如图表4所示的波特图。需要说明的是,波特图的确比较友善又比较恶心地采用了dB作为纵坐标,这个原因这里不做展开。
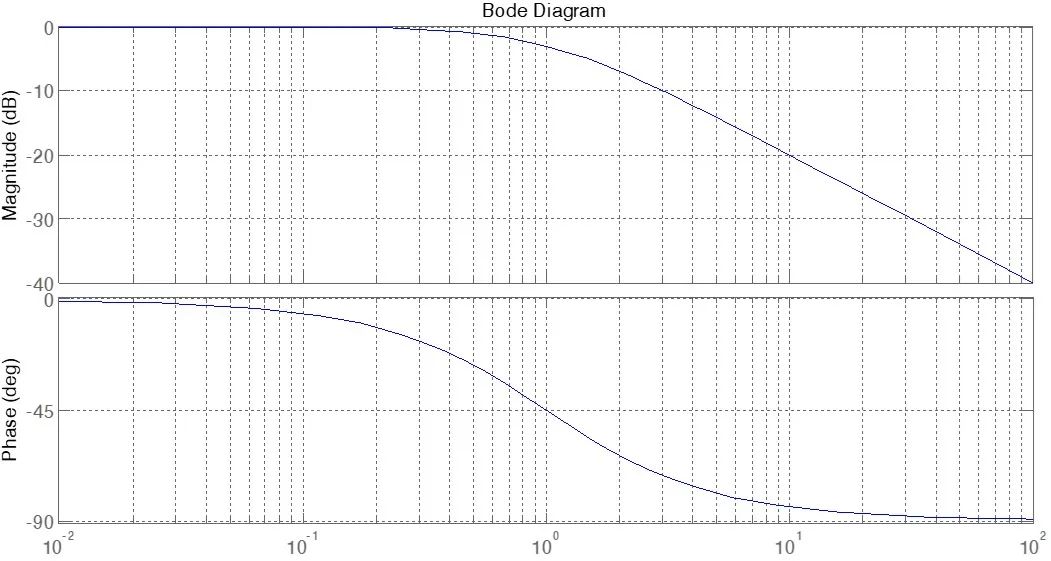
图表 4 波特图
这个图很神秘,但是的确展示了图表3所代表的系统的频率响应。至少我们可以看到,输出的幅值对频率变化很敏感,频率约高,则衰减越明显。所以,就如上篇中3.3.2所说,这个系统叫作“低通滤波器”,因为只有低频可以舒服地通过,而高频输入则会得到很大的衰减。
例如上面那个算例ω = 1和ω = 3的输入和输出,ω = 3被更明显地削弱了。
滤波器设计
这里就要提一下滤波器设计了。图表4的图告诉我们:
在ω = 1的频率,幅值衰减了0.707倍,我们也叫做滤波器的“剪切频率ωc”;
在ω = 0.1(0.1ωc)的频率,幅值衰减了0.995倍,可以基本认为没有衰减;
在ω = 10(10ωc)的频率,幅值衰减到了9.95%,可以基本认为衰减完了。
所以可以认为,当ω < 0.1时,输出没有明显衰减;当ω > 10时,输出基本衰减废了;0.1 < ω < 10时,输出有衰减,但是还不至于消失。
这个显著的频率响应很重要。如果我们需要保留的信号ω < 0.1,而需要灭除的信号ω > 10,这个滤波器无疑很合适。也就是需要灭除的信号频率/有用的信号 > 100。
这里要说一下赛思亿的变频器,开关频率是需要灭除的信号,频率一般是2.5kHz(谐波),而有用的信号一般是基波,频率一般是50Hz,则需要灭除的信号频率/有用的信号 = 50,即便我们再怎么移动这个滤波器剪切频率,或者我们另基波分量衰减,或者我们必须容忍较大分量的谐波存在。
从0.1ωc过渡到10ωc,图表4给出的幅值响应随着ω的增加衰减太平缓了。为了解决这个问题,我们需要使用更高阶的滤波器设计。
为了考察这个滤波器设计,赛思亿通常由R、C和L组成二阶正弦波滤波器,然后也大量使用波特图考察滤波器设计的特性,一个典型的幅频响应参见图表5。
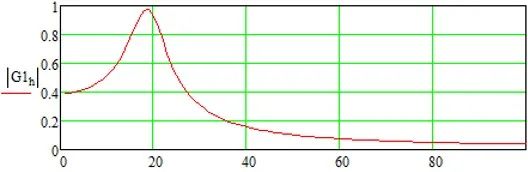
图表 5 典型的滤波器幅频响应
小 结
本篇和上篇蜻蜓点水一般写了一些关于拉普拉斯变换和傅里叶变换的一些理解,给出一些小结和感悟如下:
1、拉普拉斯变换引入了传递函数的概念,给出系统在特定输入下输出特定相应的规律总结,把一大堆一阶、二阶、稳定、不稳定系统都用传递函数方式表达了出来;
2、傅里叶变换引入了频域的概念,将一大堆杂乱无章的重复波形,用频域上的XY轴轻易分解了出来;
3、线性时不变系统和波特图利用拉普拉斯变化和傅里叶变化对电气信号的理解,给了我们方便易用的系统分析工具,尽管拉普拉斯拒了傅里叶的论文,但是两位老先生联手给了电力系统、电气信号的简洁而易用的描述方式,这些描述方式和衍生工具帮助我们理解并设计相应系统;
4、在电力推进系统中,如果出现诡异而不可捉摸的问题,那一定是我们还没理解系统,我们的电气世界已经被两位老先生阐述的足够清晰和简洁,人生的难题大部分是因为不理解,电气世界也是,尽管大学的时候饱经折磨,但还是感谢俩老头,给所有的电气人打开了一双眼睛,让我们从另外的角度看待电气世界,让我们在面对多变而难以捉摸的电气系统时,不再那么的无助。
提示:上文的观点如果难以理解,建议配合相应的专业书籍阅读,你会在某些时刻和作者一样在脑海中出现了一副3D眼镜,帮助你理解电气世界内的信号和系统,副作用是在你看某些印象派名画时,会给出不知所云“这幅画左上方的这个高频脉冲信号很突兀”,容易被专业人士追打……

 公司新闻
公司新闻 技术资讯
技术资讯 媒体报道
媒体报道

 苏公网安备 32021402001768号
苏公网安备 32021402001768号