邵博士科研随笔来自于赛思亿内部学习资料,主要是邵博士给技术人员有关技术基础的培训资料,挑选有代表性的发布,与业内的朋友共享。

拉普拉斯的那些事儿
“懂与不懂,都是收获”
背景介绍
拉普拉斯变换和傅里叶变换是所有学习电气工程的同学心中永远的痛,因为其覆盖的课程包括且不限于“基本电路理论”、“积分变换”、“自动控制原理”和“信号与系统”等。就邵博士个人而言,当时的学习有2个很直观的感觉,一来在学习过程中,完全陷入了拉普拉斯和傅里叶变换的数学公式的记忆和运算中了,二来根本搞不清这两货的区别是什么,感觉就是拉普拉斯更加高级一些而已。
作为一种经验的提炼,或者说仅仅作为一本学习笔记,本文档总结一下拉普拉斯变换对于赛思亿的工作中的一些作用。需要说明的是,本文档的观点都是邵博士个人观点,并不说明这些观点都是正确的。
拉普拉斯变换
虽然我们先学习的是傅里叶变换,但是实际上我先说的是拉普拉斯变换,原因有二,首先是拉普拉斯变换更多的只是一种数学变换,相对理解更为单纯,另外拉普拉斯比傅里叶年长19岁,先出生的。所以拉普拉斯变换实际上出现时间早。
- 1.什么是拉普拉斯变换
拉普拉斯变换本质上是一个数学工具,属于一种积分变换,即将时域t的信号,转变成了复数域s的信号。因此,拉氏系统仍然是时域系统,解决的问题也是t的问题。
从邵博士看来,拉普拉斯巧妙解决了对于信号和系统的数学描述。
-
2.信号与系统
一个信号的性质,可以很清晰地用关于t 的函数x(t)来展现出来,这是老百姓们喜闻乐见的。但是问题来了,一个例如电阻、电感和电容组成的系统,该如何描述呢?一个信号进入了系统之后的结果,又如何描述呢?
拉普拉斯是这么考虑的:
1.
信号x(t)通过拉普拉斯变换,可以转换成X(s)。
2.
一个系统,如果用一个冲击函数δ(t)作为输出,这个系统的输出G(t)进行拉普拉斯变换,就成为这个系统的所谓系统函数G(s)。
3.
信号X(s)经过系统G(s)之后的输出是Y(s) =X(s)G(s),其反变换y(t)就是输出信号。
总结来说,在拉普拉斯看来,信号和系统的本质是一样的,都是用s的一串描述。一个任何信号X(s)经过系统G(s),和一个信号G(s)经过系统X(s),结果是完全一致的。从观察者来说,信号和系统没有区别。或者说“信号即系统,系统即信号”。

皮埃尔-西蒙 拉普拉斯 Pierre-Simon Laplace 1749 ~ 1827
拉普拉斯做了很多事情,研究了概率论,做过拿破仑的老师。但是他最大的贡献是让很多21世纪的电气专业学生生活在拉普拉斯变换的恐惧中。
-
3.一阶系统分析
假设有一个一阶系统:
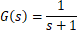
我们现在要考察一个阶跃信号x(t) = ε(t)进入这个系统之后的输出是啥样子,该如何做呢?
3.1 数学计算
如果用数学计算的方法,那么首先计算阶跃信号ε(t)的拉普拉斯变换,可以得到:
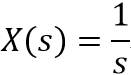
这样系统的输出为:
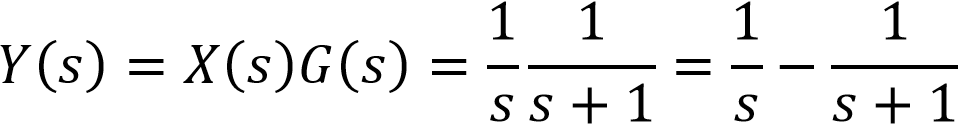
对输出进行拉普拉斯反变换,可以得到:
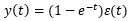
这个时域信号在t = 0的时候是0,在t = +∞的时候是1。
3.2 Matlab仿真结果
为了有更好地直观的感受,可以考察一下如图表 2的阶跃系统仿真。
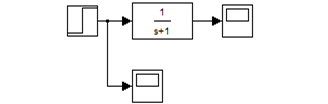
图表 2 Matlab的一阶系统阶跃仿真模型
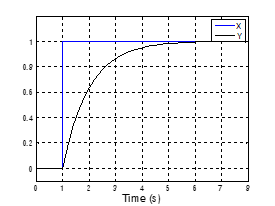
图表 3 一阶系统阶跃仿真结果
这个系统函数为
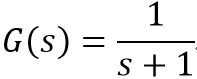 的系统又称为“一阶低通滤波器”,当然,最终讲清楚这件事情的是还没有登场的傅里叶。一阶系统可以是一阶低通滤波器,也可以是一阶高通滤波器。其中一阶低通滤波器最为常见,因此本文主要讲低通滤波器。直观地说,一阶低通滤波器就是将信号变化的速度变缓慢,从一个锋锐的阶跃变成缓慢的上升。
的系统又称为“一阶低通滤波器”,当然,最终讲清楚这件事情的是还没有登场的傅里叶。一阶系统可以是一阶低通滤波器,也可以是一阶高通滤波器。其中一阶低通滤波器最为常见,因此本文主要讲低通滤波器。直观地说,一阶低通滤波器就是将信号变化的速度变缓慢,从一个锋锐的阶跃变成缓慢的上升。3.3 一阶低通滤波器的时间常数
不失一般性,我们给出一个一阶低通滤波器的最常见的状态:
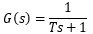
参照3.1的方法,可以得到其阶跃响应为:
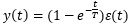
其中T就是一阶低通滤波器的时间常数。很显然,t越大,y(t)约接近于1。这个t的时间用时间常数T来衡量最合适不过。
从表格 1可以看到,当t = 3T时,y(t)达到了最终稳定值的95.0%(3T原理),当t = 5T时,y(t)达到了最终稳定值的99.3%(5T原理)。
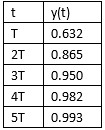
表格 1 一阶系统时间常数计算
从图表 3也可以清晰地观察到3T原理和5T原理的结果。
3.4 一阶低通滤波器的应用
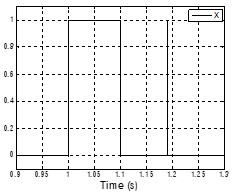
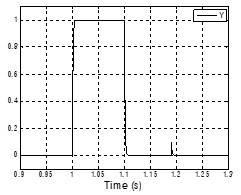
图表 4 经过一阶低通滤波器的输入和输出(左图为输入,右图为输出)
这里讨论一阶低通滤波器的一种应用。左图为一阶低通滤波器的信号输入,在1s的时候,有一个长度为100ms的有用脉冲信号进入,在1.19s时,有一个长度为0.1ms的干扰信号进入。
系统希望对有用信号进行动作,但是想消除干扰信号的影响。为了这个目的,构筑一个低通滤波器:
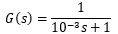
用图表 5所示的仿真模型,可以得到图表 4右图的结果。可以看到,有用信号几乎没有太大的影响,而无用的信号由于时间宽度太窄,几乎被消灭不见了。
这种滤波器的设计,关键在于时间常数T。时间常数T越大,则有用信号的失真越大,但是对干扰的抑制越明显。
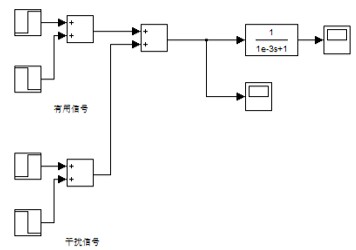
图表 5 仿真模型
赛思亿至少在2个地方使用了上述的概念:
① PPB的光电编码器滤波硬件电路设计。光电编码器的输出使用低通滤波器可以有效地减少干扰对信号的影响,特别是z通道的信号。但是需要注意的是,随着转速的升高以及分辨率的上升,有用信号脉冲宽度变窄,则时间常数T需要适当降低。
② PLC中的对于DI信号输入的滤波调整,采用软件的方式构筑低通滤波器来消除可能的干扰导致的DI误响应。
3.5 二级系统响应
看完了一阶系统响应,我们来瞅瞅二阶系统响应。假设系统函数分别为:
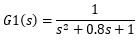 和
和 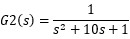
两者的阶跃响应可以从图表 6看出一些端倪。G1(s)的阶跃响应出现了超调,而G2(s)的阶跃响应和一阶系统的阶跃响应类似,只不过更慢。
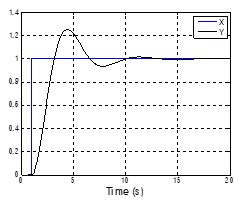
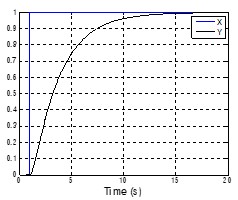
图表 6 G1(s)和G2(s)的阶跃响应
二阶系统和一阶系统不同的是,一阶系统永远是稳定的,而二阶系统有可能是振荡的,可能是稳定但是具有超调,也可能是稳定但是没有超调,要复杂的多。
所以教科书里面,往往会针对不同的二级系统,定义所谓的“振荡系统”、“无阻尼系统”、“欠阻尼系统”、“临界阻尼系统”和“过阻尼系统”等等。这些分析就不展开了。总之来说,二级系统更加复杂。
-
4.系统函数有什么用
现在简单展开一下,系统函数或者说拉普拉斯变换还有哪些用处呢?由于系统函数本质上是对一个系统进行了一个深度的数学描述,因此最大的优势就是可以用数学的计算定量地考察一个系统的性能。特别的,可以用来考察一个系统的稳定性。
系统的稳定性,经典控制系统用所谓的极点来分析。一个控制系统,首先要追求整体系统的稳定性,一般采用闭环传递函数来表达。事实上闭环传递函数在控制器设计出来之前并不知道,所以一般采分析分析开环传递函数的零极点,就可以知道控制的主要参数设计。这时候,一些经典的工具,类似根轨迹法、奈奎斯特曲线法和罗素判据啥的就出来了,其实没有啥实际工程作用。
我们花了精力解释了一下一阶系统和二阶系统。实际上,很多系统都是高阶的,但是只要关注最右边的极点,一般高阶系统都可以凑凑合合近似成一阶系统或者二阶系统。
然而这些系统通常仍然不实用,因为上面所有描述的系统都属于“线性时不变系统”,那些不属于线性时不变系统都属于超纲题了,考试不考的。可惜的是,绝大部分的系统都是这种讨厌的非线性系统,一般来说,要定性分析这些非线性系统就很难了,更不要说什么零极点了。如果一定要分析,那么就会用小信号模型等方法进行线性化处理。这里不多扯淡了,因为邵博士认为小信号模型方法本身就没啥用。

 公司新闻
公司新闻 技术资讯
技术资讯 媒体报道
媒体报道

 苏公网安备 32021402001768号
苏公网安备 32021402001768号